この記事は、ToBuToRiが統計検定準1級受験まで学習した軌跡を残す記事になります。
のちに統計検定準1級を受験しようかと考えている人が見たときに、学習計画や学習内容の参考になることを目指します。
ToBuToRiの理解を深める意味も込めて、学習内容を定期的にまとめて記事にしたいと思っています。
※記事中の数式は、LaTeXで書いています。
今週学んだのは、
- 2次元のデータ(相関)
です。
それでは、行ってみましょう。
相関
2次元のデータとは、一つの変数\(x\)ではなく、2変数\(x\)、\(y\)を観測して得られたデータです。
相関とは、この2変数\(x\)と\(y\)の間に区別を設けずに対等にみる見方や方法のことを言います。
散布図
散布図とは、観測対象\(x\)と\(y\)が対になる量的データである場合に、横軸に\(x\)、縦軸に\(y\)を取って、各観測対象を平面上にプロットすることで、視覚的に関係を把握するものです。
散布図の作成は、2次元データの分析で普通最初に行われます。
散布図を見ることにより、\(x\)と\(y\)が何かしらの関係を持っているのか、それともそうでないのかを識別することが出来ます。
都道府県別での総人口に関する面積と15歳未満人口の相関は下記のようになり、総人口と面積には関係性がないが、総人口と15歳未満人口には関係性があるように見えます。
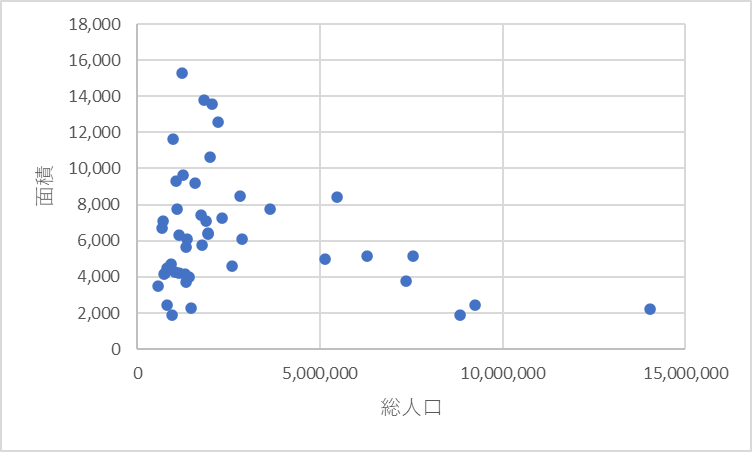
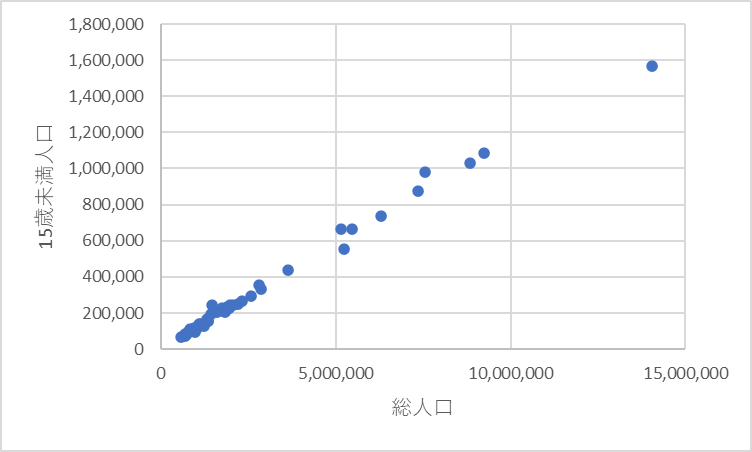
相関関係
二つの変数間の関係のことを一般的に相関関係と呼びます。
特に統計学ではこの相関関係が直線に近い傾向がみられる場合に、相関関係があるといいます。
図2のように、一方の変数が増加するにつれて他方の変数も増加する場合、「正の相関関係がある」と言います。
図3のように、一方の変数が増加するにつれて他方の変数が減少する場合、「負の相関関係がある」と言います。
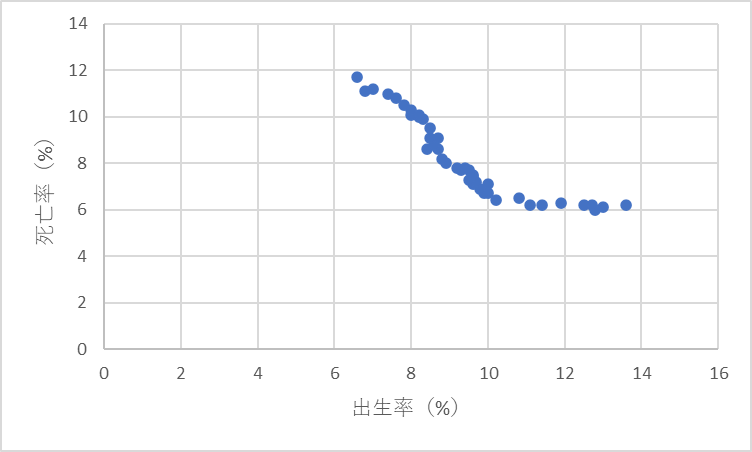
直線的な傾向の程度を「強い」「弱い」と表現します。
また、図1のようなものは、「相関関係がない」と言います。
分割表
二つのデータが量的データの場合は散布図を書くことが出来ますが、片方、あるいは両方とも質的データの場合には分割表と呼ばれる手法を取ります。
分割表は、表1のように質的データを集計した表になります。
| 日本人 | 留学生 | 合計 | |
| 修士課程 | 2,415 | 274 | 2,689 |
| 博士課程 | 2,002 | 620 | 2,622 |
| 合計 | 4,417 | 894 | 5,311 |
また、分割表は、社会調査やアンケート調査の結果分析で良く用いられる方法で、それぞれのデータをクロスさせて両者の関係を見ることからクロス表とも呼ばれます。
相関表
二つのデータのうち、一方が量的データの場合に、量的データを適当な階層に分けて項目化することで、分割表を作ることが出来ます。
両方のデータが量的データの場合にも、適当な階級に分けることで分割表を作ることが出来て、特に相関表と呼ばれます。
相関係数
二つのデータの相関関係は、散布図で見て取る以外に、相関係数(積率相関係数)にて定量的に測ることが出来ます。
相関係数は、
$$ r_{xy} = \frac{\sum(x_i – \bar{x})(y_i – \bar{y})/n}{\sqrt{\sum{(x_i – \bar{x})^2/n}}\sqrt{\sum{(y_i – \bar{y})^2/n}}} = \frac{\sum(x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum{(x_i – \bar{x})^2}}\sqrt{\sum{(y_i – \bar{y})^2}}} $$
で定義されます。
相関係数が1に近づくほど正の相関があり、-1に近づくほど負の相関があります。
共分散
相関係数の定義の分母の\(\sqrt{\sum{(x_i – \bar{x})^2/n}}\)、\(\sqrt{\sum{(y_i – \bar{y})^2/n}}\)は、変数\(x\)、\(y\)のそれぞれの標準偏差\(S_x\)、\(S_y\)となります。
これに対して分子\(C_{xy} = \sum(x_i – \bar{x})(y_i – \bar{y})/n\)を共分散と呼びます。
相関関係と因果関係
相関係数が高いということは強い相関関係があることになりますが、二つのデータの間に因果関係があるかどうかとは関係がありません。
偏相関係数
二つのデータに相関関係がある場合でも、別のデータを介して相関関係がある場合があります。
例えば、ある駅前の飲食店の数と銀行の数に相関関係があったとします。
それは、各々が昼間の人口に相関関係を持っているという場合です。
その場合の相関関係はみかけ上の相関と呼ばれることもあります。
そういった場合には、変数1から変数3までの三つの変数があるとき、変数3の影響を除いた後の変数1と変数2の間の相関係数を見るとよく、これを偏相関係数と呼びます。
$$ r_{12\cdot3} = \frac{r_{12} – r_{13}r_{23}}{\sqrt{1 – {r_{13}}^2}\sqrt{1 – {r_{23}}^2}} $$
順位相関係数
相関係数(積率相関係数)はデータがともに量的データである場合に用いられますが、二つの質的基準がある場合に、それぞれの基準における順位の間の相関を示す指標として順位相関係数があります。
順位相関係数には、スピアマンの定義とケンドールの定義があり、それぞれ
$$ r_s = 1- \frac{6\sum_{i=1}^n(d_i)^2}{n^3 – n} (d_i:各観測対象の順位差)$$
$$ r_K = \frac{G-H}{n(n-1)/2} (G:観測対象の対が正順である数、H:観測対象の対が逆順である数)$$
と計算することが出来て、同順位がある場合は一定の方法でこれを修正することになります。
時系列データと自己相関係数
時間的に観測されたデータを時系列データと言います。
時系列データに関しては、同じ系列のデータの異なる点の相関関係を見ることになります。
その関係を表すものが自己相関係数です。
h時点遅れたデータとの自己相関係数は、
$$ r_h = \frac{\sum_{i=1}^{n-h}(x_i-\bar{x})(x_{i+h}-\bar{x})/(n-h)}{\sum_{i=1}^n(x_i-\bar{x})^2/n} $$
となります。
この自己相関係数から時系列データの季節性が読み取れ、各時点での自己相関係数をグラフにしたものをコレログラムと言います。
まとめ
今回は学んだのは、
- 2次元のデータ(相関)
です。
【学習を開始して32日目】
では、また。













